压力变送器介绍非线性振动的基本特性

      前面压力变送器介绍的动力计算中提到一个方程如图1所示。在这个方程中，惯性力、阻尼力和弹性力均为线性、常系数的.应用这个方程能够解决许多实际的问题.但是机械系统振动(riIJ题中有许多现象无法用线性振动理论来解释。例如。由于大位移而导致的几何非线性。或由于限尼力、弹簧力的因素产生的物理非线性。这类问题的运动方程是非线性的，故称为I卜线性振动问题。

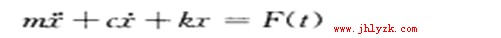
      引起非线性振动的原因很多。主要是非线性恢复力和非线性阻尼力所致。
      非线性恢复力(弓单性力)是指弹性元件材料的力与变形不成线性关系或山于JL何构造原因造成的恢复力与位移的关系不成线性.非线性Pit尼力则说明某些振动系统中复杂的阻尼不能通过前面所述简化方式线性化处理。
      非线性振动有许多一与线性振动完全不同的从本性质，现择要简单介绍如下.
      I)振动倾率随振幅变叮匕
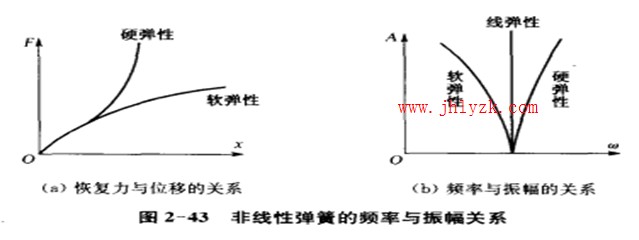
      恢复力为非线性时，系统的tAi有频率随振福的大小而变化.压力变送器发现这与线性系统固有频率f义与系统参数有关的性质完全不同。如非线性弹性为硬弹性(弹性系数随位移增大而提高)。Nut频率陆振幅增大而提高;反之，如为软弹性。则倾率随振幅增大而减"1",图2-43所示为非线性弹簧的变形一恢复力关系和且有非线性恢复力系统的频率一振幅关系。

则振幅又将从C点升到d点。又发生一次突变。然后再助板率的减小而趋向于朴位移依.对于软弹性的非线性系统.也会发生类似的现象.

      非线性受迫振动中振幅肋激振力颇率变化而发生的这种突变现象称为跳跃现象。在激振领率由小到大渐变和由大到小渐变时。探幅变化的过程不4411-1.这些现象在线性振动系统.书，是不会发生的。
      3)次玄咨名吸动和超i啼才长动
      一个线性的机械系统。在简t皆激振力Fsin的作用下。它的受迫报动仅包含倾率为.的谐波响应.当激振力孩率。接近系统固有频率二时。系统只出现与干扰力频率相I司的共振.但对于非线性机械系统而言。情况就不同。在简i许力Fsin作用下。系统的受迫振动
不仅包含频率为。的谐波响应，还会有倾率为号的次谐波响应和预率为”.的妞谐波响应《为正整数).系统中究竟会发生哪些次i皆振动和超谐振动。耍视具体条件而定.由于次i片和超i杆振动的存在，非线性系统中除了会发生激振倾率.接近于系统固有狈率.。的i片波
共振外，还会发生。.的超谐共振或誉的次1W共振·因此·非线性系统的响应颇率数目超过了系统的门山度数目。较之线性系统有更多的发生共振的可能性.
      4)女且合奴率振动
      非线性系统受到两个以上械率简活力激振时。会产生组合领率的受迫振动.设系统受到两个简i铸千扰力厂和Fxxin的作用，则系统不仅可能有倾率为。以及粉赞的受迫振动响应，还会出现毅率为组合颇率动儿中。差压变送器计算他们的和为正枯数。
      5》叠加原理不适用
      线性系统中可川登加原理处理问题。即系统在多个激掀力作用卜的响应可认为是各个激振力单独作用下系统响应的柱加。
      由非线性系统的组合倾率振动现象可知，对于非线性系统而言。畏加原理已不再适用。
求非线性系统的全解不能像求线性系统的全解那样。由求得的各个特解处加而成。系统对多个激振的响应井不是简单地对梅个激振响应的柱加。而是对这些激振的综合响应。这种情况使得寻求非线性系统的全解变得份分复杂。

      2)跳跃现象
      具有非线性弹性的机械系统。在简i片激振强迫振动时。它的幅顿曲线不同于线性系统。曲线有向右(硬弹性时)或向左(软弹性时)杏曲的现象，如图2-44所示。
      对线性系统而言，激振力辐俏保持不变而逐渐改变激振力的频率时，不论是频率值由小到大变化，还是由大到小变化，系统受迫振动幅仇的变化都是连续的〔见图2-44(a)]。但楚. R"r于非线性系统。以硬弹性为例〔见图2-44(c)].当激振力辐位不变而逐渐增加激振力颇率时，振幅也随着增大。在振幅增大到“点后。再增大频率则振幅将突然从“点降到b点。发生一个突变。如频率是从高频向低频变化，则振幅变化将沿be到达c点，再继续减低倾

下一篇：机械振动的定义与表示方法

上一篇：液压传动的工作原理